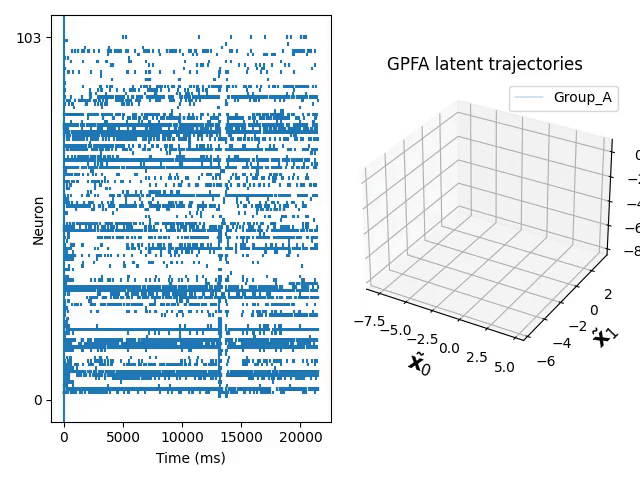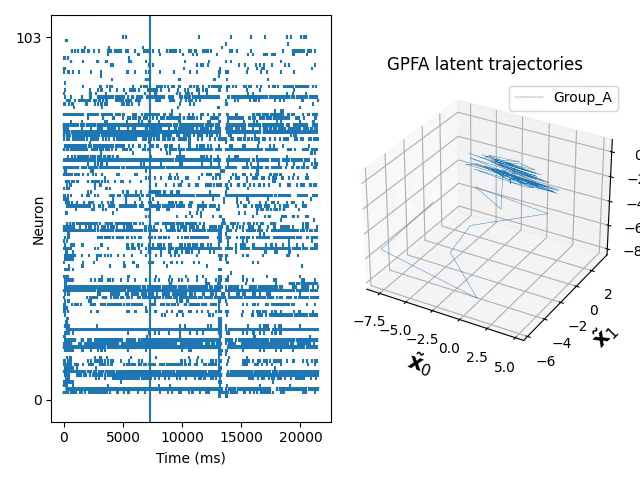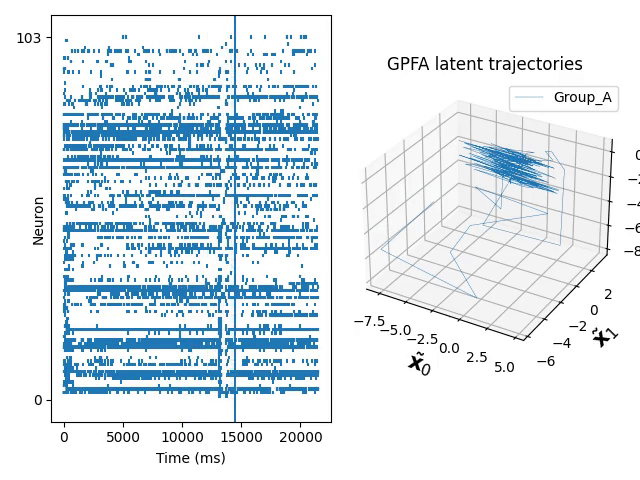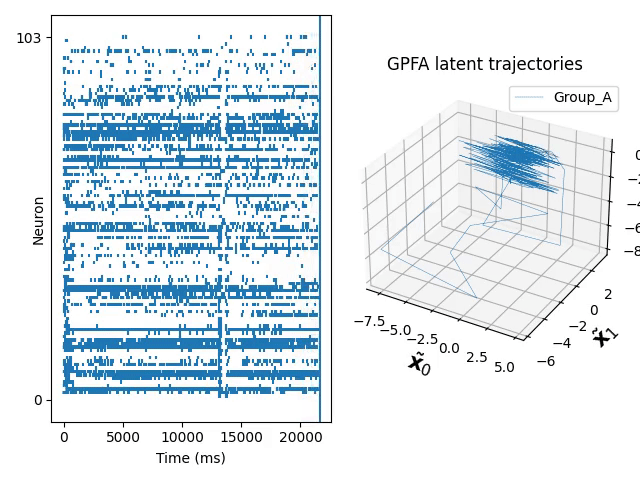
Gaussian process makes it possible to construct probabilistic models over unknown underlying functions. This is useful for modelling temporal continuous trajectories in datasets recorded from populations of neurons. Gaussian Process Factor Analysis (GPFA) is a popular technique for extracting latent trajectories to low dimensional space and making use of the Gaussian Process.
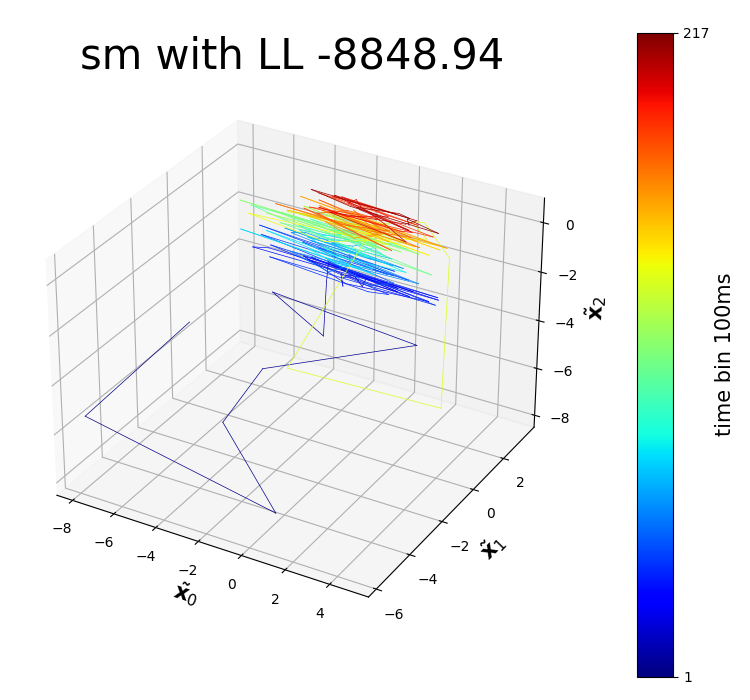
In the past, a variety of kernels have been tried on different distributions of models. Optimizing their kernel parameters while preventing numerical errors is a problem that is hard to tackle. We developed 9 kernels on the most widely used Python Elephant Neurophysiological Analysis Toolkit, optimizing kernel parameters using gradient-free Bayesian Optimization and the Powell Method. We compared the best-performed Spectral Mixture (SM) kernel (which is able to generalize all kernels) and the originally adopted RBF kernel, and found it can perform 20-70 negative log-likelihood better.
You can find the code and a tutorial to use these modified kernels in our GitHub repo. Below is a dim-reduced trajectory extracted from neuro data of a mouse who was repetitively doing the same experiment.